astrokvm.blogg.se

obtaining new ladder operators and a toy model for QFT with a minimal length.

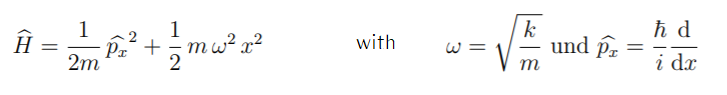
It is shown that even though our Hamiltonian is formally different from the ordinary one, it yields equivalent results for the state vectors of physical interest. The above modification results in correction terms in the Hamiltonian of. As a consequence, the number operator for the lattice quasiparticles commutes with the Hamiltonian, a property which is useful in certain applications. A lattice creation operator in this formulation actually creates a vibrational mode (in a given state) from the physical vacuum, in contrast to a ladder operator which merely generates transitions between two states of an already existing vibrational mode. A Hamiltonian is derived in this paper in which both the electrons and the lattice (in the harmonic approximation) are represented in field-theoretical formalism. The Hamiltonian for the 1D Harmonic Oscillator. The operators we develop will also be useful in quantizing the electromagnetic field. Operator methods are very useful both for solving the Harmonic Oscillator problem and for any type of computation for the HO potential. Although the equal spacing of the harmonic-oscillator energy levels and the commutation relations satisfied by the oscillator ladder operators have led to an interpretation of this formalism in terms of the "creation and annihilation" of phonons, the phonons thus defined are not the quasiparticles which are obtained by a field-theoretical formulation of the lattice Hamiltonian in the harmonic approximation. Harmonic Oscillator Solution using Operators. +q \right )\]įrom this we can get our equation (we won't do it here) for the energy of an our eigenvaules.The Hamiltonian most often used to describe a system of electrons interacting with lattice vibrations has the asymmetry that the electrons are represented by the creation and annihilation operators which arise from quantum field theory whereas the lattice vibrations are represented by the one-particle ladder operators of the one-dimensional harmonic-oscillator problem. We also relate the different ladder operators obtained by various combinations of supersymmetric constructions involving Darboux-Crum and Krein-Adler.